معیارها برای انتخاب آزمون های آماری
در مطالعه FellowsMaxwell2019 داده هایی که دارای Skew بودند ابتدا لگاریتم گرفته شده و بعد وارد آنالیز آماری شده اند.
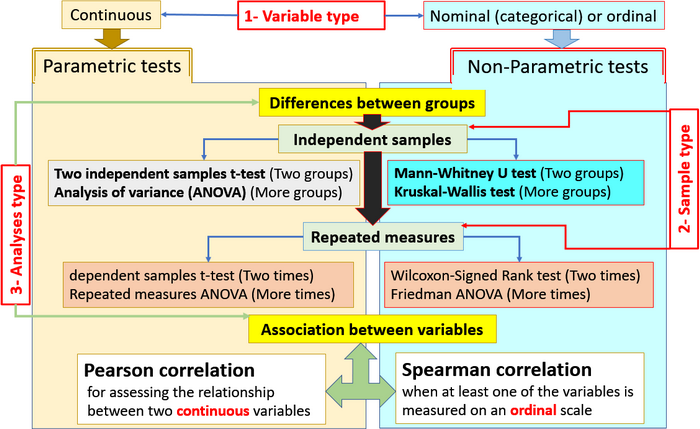
Criteria for Selection of statistical tests
Mann Whitney U Test=Wilcoxon Rank Sum Test=Mann Whitney Wilcoxon Test
Kolmogorov-Smirnov test | Shapiro–Wilk test | Two-sided t-test for continuous variable, Fisher’s exact test for categorical variable Bonferroni corrected P | Pearson test |
Data were shown as mean (standard deviation, SD) or median (interquartile range, IQR).
Chi-square or, when necessary, Fisher exact test, were employed to explore the association between categorical variables
Two way ANOVA
Cochran's Q test | Hazra_2016.pdf | chi-squared cannot be used to test correlated data (like matched pairs or panel data). In those cases, McNemar's test may be more appropriate. |
It is desirable that for the normal distribution of data the values of skewness should be near to 0. What if the values are +/- 3 or above?
Tab Navigation on W3.com
To perform a test of significance between means of two groups is well known. But if I use the medians is it possible to test for significance between medians of two groups?
Fisher's Exact test in SPSS (Fa)
Types of variables
A variable is a characteristic that can be measured and that can assume different values. Height, age, income, province or country of birth, grades obtained at school and type of housing are all examples of variables. Variables may be classified into two main categories: categorical and numeric. Each category is then classified in two subcategories: nominal or ordinal for categorical variables, discrete or continuous for numeric variables. These types are briefly outlined in this section.
Categorical variables
A categorical variable (also called qualitative variable) refers to a characteristic that can’t be quantifiable. Categorical variables can be either nominal or ordinal.
Nominal variables
A nominal variable is one that describes a name, label or category without natural order. Sex and type of dwelling are examples of nominal variables. In Table 4.2.1, the variable “mode of transportation for travel to work” is also nominal.
Ordinal variables
An ordinal variable is a variable whose values are defined by an order relation between the different categories. In Table 4.2.2, the variable “behaviour” is ordinal because the category “Excellent” is better than the category “Very good,” which is better than the category “Good,” etc. There is some natural ordering, but it is limited since we do not know by how much “Excellent” behaviour is better than “Very good” behaviour.
It is important to note that even if categorical variables are not quantifiable, they can appear as numbers in a data set. Correspondence between these numbers and the categories is established during data coding. To be able to identify the type of variable, it is important to have access to the metadata (the data about the data) that should include the code set used for each categorical variable. For instance, categories used in Table 4.2.2 could appear as a number from 1 to 5: 1 for “very bad,” 2 for “bad,” 3 for “good,” 4 for “very good” and 5 for “excellent.”
Numeric variables
A numeric variable (also called quantitative variable) is a quantifiable characteristic whose values are numbers (except numbers which are codes standing up for categories). Numeric variables may be either continuous or discrete.
Continuous variables
A variable is said to be continuous if it can assume an infinite number of real values within a given interval. For instance, consider the height of a student. The height can’t take any values. It can’t be negative and it can’t be higher than three metres. But between 0 and 3, the number of possible values is theoretically infinite. A student may be 1.6321748755 … metres tall. In practice, the methods used and the accuracy of the measurement instrument will restrict the precision of the variable. The reported height would be rounded to the nearest centimetre, so it would be 1.63 metres. The age is another example of a continuous variable that is typically rounded down.
Discrete variables
As opposed to a continuous variable, a discrete variable can assume only a finite number of real values within a given interval. An example of a discrete variable would be the score given by a judge to a gymnast in competition: the range is 0 to 10 and the score is always given to one decimal (e.g. a score of 8.5). You can enumerate all possible values (0, 0.1, 0.2…) and see that the number of possible values is finite: it is 101! Another example of a discrete variable is the number of people in a household for a household of size 20 or less. The number of possible values is 20, because it’s not possible for a household to include a number of people that would be a fraction of an integer like 2.27 for instance.